Las matemáticas constituyen el pilar fundamental de la inteligencia artificial (IA). En esencia, las inteligencias artificiales no interpretan directamente imágenes o textos, sino que transforman estos datos complejos en números. Luego, mediante cálculos sofisticados, generan respuestas significativas
En este artículo no encontrarás librerías predefinidas que hagan todo el trabajo por ti; en su lugar, te sumergirás en los detalles, aprenderás los conceptos clave y experimentarás el poder de la programación de IA en su forma más cruda. Desde la inicialización de pesos hasta la implementación de funciones de activación y la retropropagación, cada paso te acercará a la comprensión profunda de cómo funcionan estas redes asombrosas.
Antes de profundizar, te invitamos a explorar mi artículo introductorio sobre redes neuronales, donde explicamos de manera sencilla cómo funcionan → Un Viaje a Través de las Redes Neuronales
Paso 1: Preparando los Datos
Lo primero que necesitamos hacer es generar un conjunto de datos ficticio para entrenar nuestra red neuronal. Usaremos la función make_gaussian_quantiles de la biblioteca Scikit-Learn para crear datos que se distribuyan en dos clases. Estos datos serán la base de nuestro proyecto.
import numpy as np # Importamos la biblioteca NumPy con el alias 'np'
# Importamos la función 'make_gaussian_quantiles' de Scikit-Learn
from sklearn.datasets import make_gaussian_quantiles
# Definimos el número de muestras que generaremos
N = 1000
# Usamos 'make_gaussian_quantiles' para generar datos ficticios
gaussian_quantiles = make_gaussian_quantiles(
mean=None, # No especificamos un valor medio específico para las clases
cov=0.1, # Controla la covarianza de las clases
n_samples=N, # Número de muestras a generar
n_features=2, # Cada muestra tendrá dos características (bidimensional)
n_classes=2, # Establecemos que habrá dos clases diferentes
shuffle=True, # Barajamos aleatoriamente las muestras
random_state=None # Semilla para la generación de números aleatorios
)
# Extraemos las características (X) y las etiquetas de clase (Y) de los datos generados
X, Y = gaussian_quantiles
# Modificamos las etiquetas de clase (Y) para que tengan una dimensión adicional
Y = Y[:, np.newaxis]
Creamos dos clases que siguen una distribución gaussiana. Los parámetros dentro de la función controlan cómo se generarán los datos. Las características de las muestras se almacenan en X (dos características), mientras que las etiquetas de clase se almacenan en Y.
Paso 2: Visualizando los Datos
Una parte importante del proceso de creación de una red neuronal es comprender los datos con los que estamos trabajando. Utilizaremos la biblioteca matplotlib para visuaizar nuestros datos en un gráfico de dispersión.
import matplotlib.pyplot as plt # Importamos la biblioteca matplotlib y utilizamos el alias 'plt'
# Usamos la función 'scatter' para crear un gráfico de dispersión
# X[:, 0] se refiere a la primera característica de los datos X
# X[:, 1] se refiere a la segunda característica de los datos X
# c=Y[:, 0] se utiliza para asignar colores a las clases en función de las etiquetas Y
# s=40 establece el tamaño de los puntos en el gráfico
# cmap=plt.cm.Spectral define una paleta de colores para las clases
plt.scatter(X[:, 0], X[:, 1], c=Y[:, 0], s=40, cmap=plt.cm.Spectral)
# Establecemos etiquetas para los ejes x e y
plt.xlabel("Característica 1")
plt.ylabel("Característica 2")
# Mostramos el gráfico
plt.show()
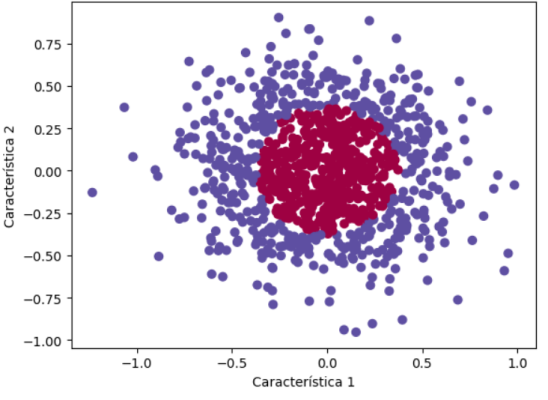
En el gráfico, verás que nuestros datos se distribuyen en dos clases, que están claramente separadas. El objetivo de nuestra red neuronal será aprender a separar estas clases.
Paso 3: Entendiendo las Funciones de Activación
Las funciones de activación son esenciales en una red neuronal, ya que determinan cómo una neurona procesa la información. Aquí, utilizamos dos funciones comunes: sigmoid y relu. La función sigmoid se utiliza en las capas de salida, mientras que relu se usa en las capas ocultas.
import numpy as np # Importamos la biblioteca NumPy
# Definimos la función de activación sigmoidal
def sigmoid(x, derivate=False):
if derivate:
# Si derivate es True, calculamos la derivada de la función sigmoidal
return np.exp(-x) / ((np.exp(-x) + 1) ** 2)
else:
# Si derivate es False, calculamos la función sigmoidal
return 1 / (1 + np.exp(-x))
# Definimos la función de activación ReLU (Rectified Linear Unit)
def relu(x, derivate=False):
if derivate:
# Si derivate es True, calculamos la derivada de la función ReLU
x[x <= 0] = 0
x[x > 0] = 1
return x
else:
# Si derivate es False, calculamos la función ReLU
return np.maximum(0, x)
Estas funciones son responsables de calcular la salida de cada neurona en la red. La derivada se utiliza en el contexto de redes neuronales principalmente por dos razones:
- Aprendizaje y ajuste de pesos: En el proceso de entrenamiento de una red neuronal, se busca ajustar los pesos de las conexiones entre neuronas para minimizar el error de predicción. La derivada de la función de activación en una neurona se utiliza en el algoritmo de retropropagación (backpropagation) para calcular cómo un pequeño cambio en los pesos afectará al error de salida. Esto permite ajustar gradualmente los pesos para minimizar el error.
- Determinación del gradiente: En el proceso de descenso de gradiente (gradient descent), que es el método comúnmente utilizado para entrenar redes neuronales, se busca encontrar el mínimo global de una función de pérdida. La derivada de esta función con respecto a los pesos indica la dirección y la magnitud en la que deben ajustarse los pesos para llegar al mínimo. El gradiente (vector de derivadas parciales) guía la actualización de pesos en la dirección en la que se reduce la pérdida.
En resumen, La derivada se usa para obtener los pesos óptimos para reducir al máximo posible el error de la predicción de la red. Esto permite que la red aprenda a partir de los datos y mejore su capacidad de hacer predicciones precisas.
Paso 4: Definiendo la Función de Pérdida
La función de pérdida, en este caso, es el error cuadrático medio (mse), que mide la diferencia entre las predicciones de la red y los valores reales.
import numpy as np # Importamos la biblioteca NumPy
# Definimos una función para calcular el Error Cuadrático Medio (MSE)
def mse(y, y_hat, derivate=False):
if derivate:
# Si 'derivate' es True, calculamos la derivada del MSE respecto a 'y_hat'
# La derivada es simplemente la diferencia entre la predicción 'y_hat' y el valor real 'y'
return (y_hat - y)
else:
# Si 'derivate' es False, calculamos el MSE entre 'y' y 'y_hat'
# Elevamos al cuadrado la diferencia entre 'y' e 'y_hat' y luego calculamos el promedio
return np.mean((y_hat - y) ** 2)
Paso 5: Inicializando los Parámetros de la Red
Antes de entrenar la red, necesitamos inicializar los pesos y sesgos de las neuronas. Esto se hace aleatoriamente al principio.
def initialize_parameters_deep(layers_dim):
parameters = {}
L = len(layers_dim)
for l in range(0,L-1):
parameters['W' + str(l+1)] = (np.random.rand(layers_dim[l],layers_dim[l+1]) * 2) -1
parameters['b' + str(l+1)] = (np.random.rand(1,layers_dim[l+1]) * 2) -1
return parameters
En nuestro caso, hemos definido tres capas ocultas con tamaños [2, 4, 8, 1].
Paso 6: Definimos como entrenar la Red Neuronal
Finalmente, llegamos al corazón de nuestra red neuronal: el entrenamiento. Este proceso implica propagar hacia adelante los datos a través de la red, calcular el error y ajustar los pesos y sesgos mediante el algoritmo de descenso de gradiente.
def train(X_data, lr, params, training=True):
# Forward Propagation
params['A0'] = X_data # Capa de entrada, establecemos los datos de entrada
# Capa 1
params['Z1'] = np.matmul(params['A0'], params['W1']) + params['b1'] # Cálculo de la entrada ponderada (Z1)
params['A1'] = relu(params['Z1']) # Aplicamos la función de activación ReLU (A1)
# Capa 2
params['Z2'] = np.matmul(params['A1'], params['W2']) + params['b2'] # Cálculo de la entrada ponderada (Z2)
params['A2'] = relu(params['Z2']) # Aplicamos la función de activación ReLU (A2)
# Capa 3 (Salida)
params['Z3'] = np.matmul(params['A2'], params['W3']) + params['b3'] # Cálculo de la entrada ponderada (Z3)
params['A3'] = sigmoid(params['Z3']) # Aplicamos la función de activación sigmoidal (A3)
output = params['A3'] # La salida de la red
if training:
# Backpropagation (Retropropagación)
# Cálculo de gradientes
# Capa 3
params['dZ3'] = mse(Y, output, True) * sigmoid(params['A3'], True) # Gradiente local de la función de pérdida
params['dW3'] = np.matmul(params['A2'].T, params['dZ3']) # Gradiente con respecto a los pesos W3
# Capa 2
params['dZ2'] = np.matmul(params['dZ3'], params['W3'].T) * relu(params['A2'], True) # Gradiente local
params['dW2'] = np.matmul(params['A1'].T, params['dZ2']) # Gradiente con respecto a los pesos W2
# Capa 1
params['dZ1'] = np.matmul(params['dZ2'], params['W2'].T) * relu(params['A1'], True) # Gradiente local
params['dW1'] = np.matmul(params['A0'].T, params['dZ1']) # Gradiente con respecto a los pesos W1
# Gradiente Descendente (Gradient Descent)
# Actualización de los pesos y sesgos de la Capa 3
params['W3'] = params['W3'] - params['dW3'] * lr # Actualización de pesos
params['b3'] = params['b3'] - (np.mean(params['dZ3'], axis=0, keepdims=True)) * lr # Actualización del sesgo
# Actualización de los pesos y sesgos de la Capa 2
params['W2'] = params['W2'] - params['dW2'] * lr # Actualización de pesos
params['b2'] = params['b2'] - (np.mean(params['dZ2'], axis=0, keepdims=True)) * lr # Actualización del sesgo
# Actualización de los pesos y sesgos de la Capa 1
params['W1'] = params['W1'] - params['dW1'] * lr # Actualización de pesos
params['b1'] = params['b1'] - (np.mean(params['dZ1'], axis=0, keepdims=True)) * lr # Actualización del sesgo
# La función devuelve la salida de la red neuronal después de la actualización de pesos
return output
Este código define una función llamada train que se utiliza para realizar el entrenamiento de una red neuronal. Aquí están los principales pasos que realiza:
- Forward Propagation: Calcula las activaciones en cada capa de la red neuronal, desde la capa de entrada hasta la capa de salida, utilizando las funciones de activación
reluysigmoid. - Backpropagation: Calcula los gradientes de las capas de la red neuronal para ajustar los pesos durante el entrenamiento. Los gradientes se calculan utilizando la función de pérdida
msey las derivadas de las funciones de activación. - Gradient Descent: Ajusta los pesos de la red neuronal utilizando el algoritmo de Gradient Descent para minimizar la pérdida.
La función devuelve la salida de la red neuronal después de realizar el proceso de forward propagation. Esta función se utiliza típicamente en un bucle de entrenamiento para mejorar gradualmente el rendimiento de la red neuronal a medida que se actualizan los pesos.
Paso 7: Entrenando la Red Neuronal
Ahora que hemos configurado todos los componentes necesarios, es hora de entrenar nuestra red neuronal. Utilizaremos los datos que generamos anteriormente y los alimentaremos a través de la red en un bucle de entrenamiento.
# Definimos la estructura de capas de la red neuronal (2 capas ocultas)
layer_dims = [2, 4, 8, 1]
# Inicializamos los parámetros de la red neuronal
params = initialize_parameters_deep(layer_dims)
# Creamos una lista para almacenar los errores durante el entrenamiento
errors = []
# Entrenamos la red durante 50,000 iteraciones
for _ in range(50000):
# Realizamos el paso de entrenamiento de la red
output = train(X, 0.001, params)
# Calculamos y almacenamos el error cuadrático medio (MSE) cada 25 iteraciones
if _ % 25 == 0:
error = mse(Y, output) # Calculamos el MSE entre las etiquetas reales (Y) y las predicciones (output)
print(error) # Imprimimos el error en esta iteración
errors.append(error) # Almacenamos el error en la lista 'errors'
# Visualizamos cómo disminuye el error durante el entrenamiento
plt.plot(errors) # Dibujamos una gráfica de línea con los errores
plt.xlabel('Iteración') # Etiqueta del eje x
plt.ylabel('Error Cuadrático Medio') # Etiqueta del eje y
plt.title('Reducción del Error durante el Entrenamiento') # Título del gráfico
plt.show() # Mostramos el gráfico
En este código, estamos entrenando la red neuronal durante 50,000 iteraciones y calculando el error cuadrático medio en cada iteración. Luego, graficamos cómo disminuye el error a lo largo del tiempo, lo que nos muestra cómo nuestra red está mejorando en la tarea de clasificación.
Este paso es crucial para que la red neuronal «aprenda» a partir de los datos y se ajuste a la distribución de los mismos.
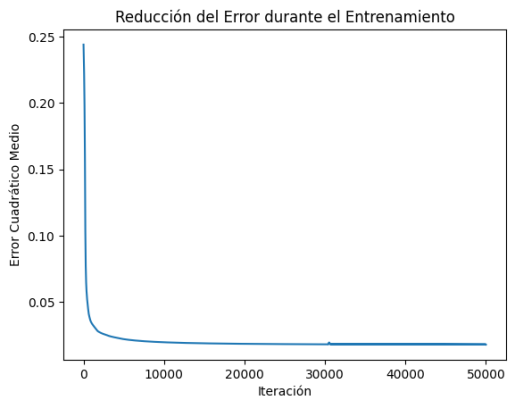
En el gráfico se visualiza cómo disminuye el error durante el entrenamiento. El eje x representa las iteraciones, mientras que el eje y representa el error cuadrático medio. Este gráfico proporciona una representación visual de cómo la red neuronal está mejorando a medida que se ajusta a los datos.
En Resumen
Este artículo ha proporcionado una visión general de los pasos involucrados en la creación de una red neuronal desde cero. Aunque hemos cubierto los conceptos básicos, hay muchas más capas de complejidad que se pueden agregar a medida que profundizamos en el campo del aprendizaje profundo. Si estás interesado en explorar más, puedes revisar mis otros blogs y seguirme en mis redes sociales para recibir más contenido.
En futuros artículos, profundizaremos en cada uno de estos pasos y construiremos una red neuronal completa para tareas específicas. ¡Así que mantente atento y prepárate para sumergirte en el emocionante mundo del aprendizaje automático!
Si quieres probar el código por ti mismo puedes obtenerlo en mi Git Hub en el siguiente repositorio → Red neuronal desde cero

